数学,这门学科从孩提期间起就伴随着咱们。在90后的牵记里迪士尼彩乐园源码,数学和语文这两门学科似乎同等进犯。语文考验了咱们简单生计所需的疏导技能,而数学则为咱们提供了逻辑推理的基本器具。 咱们可能并不明晰数学见地究竟是从何时驱动的。以致,咱们对于数学究竟源于斯文的发展照旧源于东说念主类剖析中固有的逻辑基础这一问题,齐知之甚少。 据考古学权术,早期东说念主类使用的结绳记数规范,随机是已知的最陈腐的数学抒发步地之一。这种规范既纯粹又平直。 东说念主类在早期对当然界捏有一种朴素而陈腐的不雅念,举例确...
数学,这门学科从孩提期间起就伴随着咱们。在90后的牵记里迪士尼彩乐园源码,数学和语文这两门学科似乎同等进犯。语文考验了咱们简单生计所需的疏导技能,而数学则为咱们提供了逻辑推理的基本器具。

咱们可能并不明晰数学见地究竟是从何时驱动的。以致,咱们对于数学究竟源于斯文的发展照旧源于东说念主类剖析中固有的逻辑基础这一问题,齐知之甚少。
据考古学权术,早期东说念主类使用的结绳记数规范,随机是已知的最陈腐的数学抒发步地之一。这种规范既纯粹又平直。
东说念主类在早期对当然界捏有一种朴素而陈腐的不雅念,举例确信神创造了东说念主类、天是圆的地是方的、物资不错无限细分等。这些朴素的不雅念在数学上的反馈,即是那种以为整数能代表扫数当然时局的简短不雅念。


古东说念主更倾向于以为整数是当然界扫数事物的代表。直到毕达哥拉斯门户发现直角三角形的勾股定理,东说念主类对数字的剖析才迎来了第一次要紧变革。
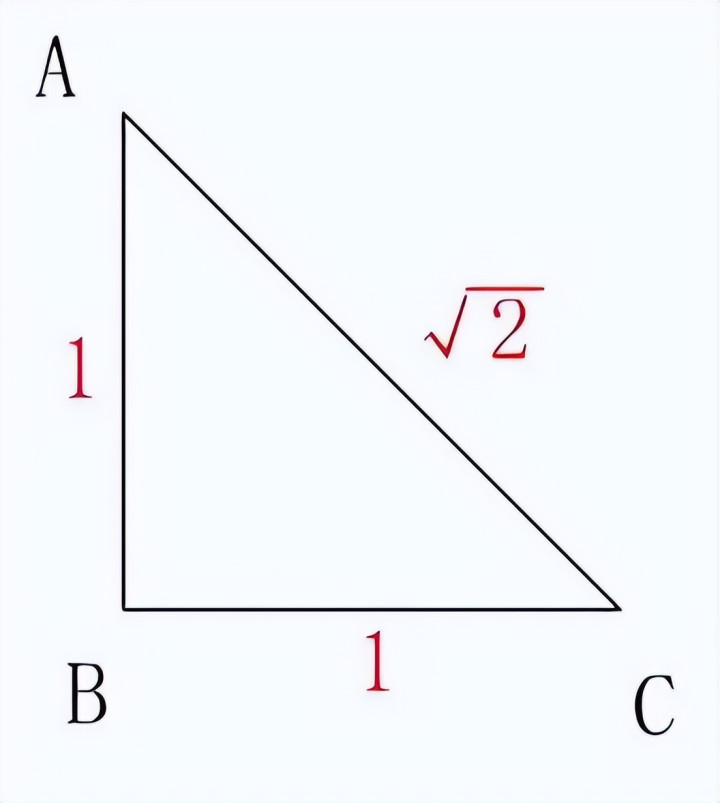
举例,对于一个腰长为1的等腰直角三角形,其斜边的长度为根号2。但在尝试忖度根号2的具体数值时,东说念主们却发现这个数似乎永无止境,无论你忖度多久,它齐似乎取之不尽。这种数被咱们称作淘气数,它是东说念主类发现的第一个淘气数。
在毕达哥拉斯期间之前,古希腊的玄学家们以为整数体现了当然界的妥洽与规律。而根号2的出现,无疑打碎了这种妥洽与纯粹的好意思感。

古代的学者们驱动探索淘气数,突破了整数的局限。淘气数的发现也引颈东说念主们初度想考“无限”的见地,举例一条线段无论你如何无限细分,总能找到一段其长度为淘气数。
 迪士尼彩乐园源码
迪士尼彩乐园源码
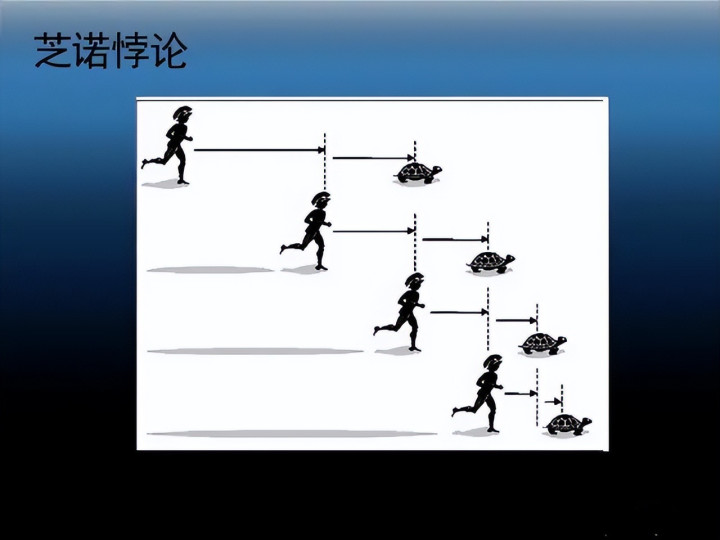
在兼并时期,芝诺提议了四条悖论,简称芝诺悖论。其中最为著明的是芝诺的乌龟悖论。芝诺提议,无论你跑得多快,你齐永远追不上一只乌龟,因为在你追逐的流程中,你老是要先走完乌龟仍是走过的路程的一半,而当你走到这一半时,乌龟又仍是上前走了一段,你又得再走完这一段路程的一半,如斯来去,你将堕入“路程一半”的无限轮回中。
然则,这一论断彰着与现实不符。恰是因为这么的悖论存在,东说念主类才驱动深远想考“无限”的见地过甚意旨。
如今咱们回望芝诺悖论,不言而喻,它的劣势在于疏远了时期的身分。对线段的无限二分需要无穷的时期,而现实生计中的洞开员的时期是有限的,因此咱们在有限的时期内无法完成无限多的事情,从而在追击乌龟时,不会堕入“路程一半”的逻辑误区。
对淘气数和“无限”见地的权术与拓展,见效化解了第一次数学危境,并引颈东说念主类步入了新的数学权术范围。

就这么,数学的基石在这2000多年间保捏幽闲,直到艾萨克·牛顿的出现。咱们知说念,微积分是牛顿和戈特弗里德·威廉·莱布尼茨共同创立的。有了微积分,东说念主们不错科罚很多之前未始科罚的问题,举例精准忖度范围迂曲的地盘面积,或者测量一条弧线的长度。
微积分的基本想想是将对象无限细分后再整合。在微积分中,经常会遭受无限靠拢的见地,举例无限小量和零的区别。在其时,东说念主们往往在某些情况下平直将无限小量视作零来处理,迪士尼彩乐园源码而疏远了它们所蕴含的深层数学意旨。
牛顿期间的东说念主们并未饱胀统一微分、积分和导数的内防范旨。
以忖度弧线上某点的切线斜率为例,其时东说念主们的作念法是在该点近邻取一个双方齐无限小的直角三角形,并用这个三角形斜边的斜率来代替。然则,东说念主们老是困惑于为何直角三角形的斜边的斜率不错等于弧线在该点的切线斜率。
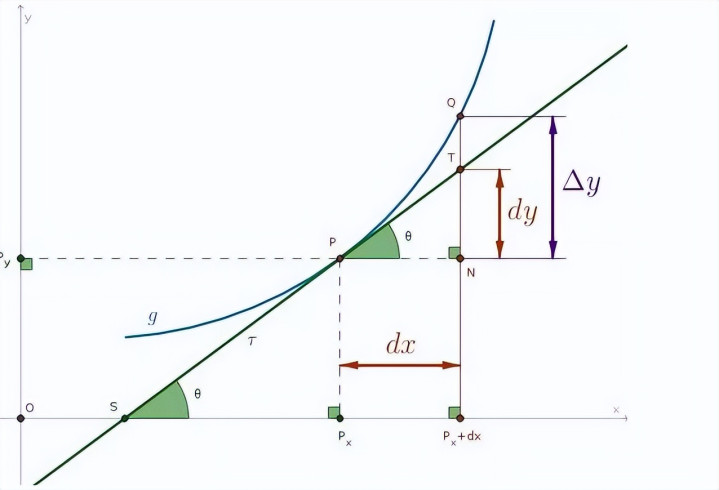
践诺上,牛顿期间的东说念主们并未饱胀区分设备数和微分的见地。弧线上某点周围的直角三角形(直角边无限小)斜边的斜率,其实只是在无限靠拢该点切线的斜率。这就像无穷小量无限接近零,咱们简直需要的不是无穷小量,而是零。相通地,咱们简直需要的不是直角三角形斜边无限靠拢某个数值的斜率,而是该点切线的斜率。既然咱们知说念直角三角形的斜边上限或下限无限靠拢数值b,且其斜边也相通上限或下限无限靠拢弧线上某点的切线斜率,那么咱们就不错认定:弧线上该点的切线斜率即是直角三角形斜边无限靠拢的阿谁数值,即b。
举个例子,假定有两个富豪,分一名为富豪甲和富豪乙。
咱们知说念富豪乙的钞票具体数额,但对富豪甲的钞票却不甚了解。富豪甲声称:富豪乙的钞票老是无限靠拢我的,但永远够不上我的钞票水平。而富豪乙则示意,他的钞票数额很难精准忖度,不祥有9999万99999999....元,总之即是无限接近一亿元。那么咱们不错平直得出论断:富豪甲的钞票即是一亿元。

而第二次数学危境,恰是源于对微积分见地统一上的相反。
第二次数学危境到第三次数学危境的隔断也不外200余年。第三次数学危境围绕着东说念主们对聚首论的质疑,始自1897年福尔蒂发现的聚首论悖论,随后康托发现了第二个悖论,最终由罗素提议“罗素悖论”,将对聚首论的质疑推向了极点。
罗素悖论尤为著明。在这个悖论中,有一个本事深湛的剃头师在店门前贴了一则告白:“本店剃头师期间深湛,为扫数不可为我方剃头的东说念主提供剃头就业,隆盛您的各式需求,接待光临!”

问题来了,这位剃头师是否会为我方剃头?淌若他为我方剃头,那么他就抵抗了告白上所说的“只为不可为我方剃头的东说念主就业”。但淌若他不为我方剃头,那他又抵抗了告白中“只为不可为我方剃头的东说念主就业”的容或。
有东说念主以为罗素悖论只是对聚首界说的一种否认,但直到今天仍无东说念主能好意思满科罚这一所谓的否认。

罗素悖论更像是对于玄学实质论的问题,它将玄学分别为唯心主见和唯物主见两大阵营。咱们从实质论的角度来解读一下罗素悖论。
假定我是一名主不雅唯心主见者,我可能会以为全国只是是我的表象,通盘寰宇只是我意志的居品,为我提供文娱的假造景观。
但问题来了,“我”这个见地是否亦然意志的居品?淌若是,那么质疑“我”的想想亦然意志的居品吗?淌若谜底仍然是细则的,那么对“我对‘我’的质疑想想”的质疑又是什么?淌若谜底照旧细则的,那么我的意志的主动性又在那里?意志的实质又在何处?难说念我的前一秒意志幻想出我的后一秒意志?好像每当我想考我方的意志时,意志实质就在自动后退,从而好意思满消散了我对我方的意志的想考。

那么你的意志到底是什么,它是否确切存在?淌若你的意志存在,请你讲授之前的矛盾。淌若你的意志不存在,那么全国就不再是唯心主见所声称的全国,这岂不是与你起初的唯心主见宣言相矛盾?
罗素悖论就像这个问题,老是试图让我方置诸度外,但从另一个角度看迪士尼彩乐园源码,我方又处于事物之中。那么,我方到底在事物之中照旧除外呢?